问题描述
最近需要分析一下不同纬度条件下惯性系对准精度,加之上月在读完《抗线晃动干扰惯性系初始对准改进参数辨识方法》后,改进了AlignMB函数,使其也具备了初始速度估计功能。刚好把高纬度对准和初始速度干扰抑制都测试一下。
对准算法
抗线运动初始对准算法非常适合用在海上摇摆基座初始对准,该方法的关键是论文中的公式(7)和(9):
\boldsymbol{v}_{sf}^{i_{b0}} = \boldsymbol{C}_{i_0}^{i_{b0}} \boldsymbol{v}_{g}^{i_0} + \left( \boldsymbol{v}_{en}^{i_b0} - \boldsymbol{v}_{en,0}^{i_b0}\right) + \boldsymbol{\omega}_{ie}^{i_b0} \times \boldsymbol{p}_{en}^{i_b0}
对其积分可得:
\boldsymbol{p}_{sf}^{i_{b0}} = \boldsymbol{C}_{i_0}^{i_{b0}} \boldsymbol{p}_{g}^{i_0} -\boldsymbol{v}_{en,0}^{i_b0} t + \boldsymbol{p}_{en}^{i_b0}+\boldsymbol{V}
对准的关键就是利用IMU数据完成 \boldsymbol{v}_{en,0}^{i_b0} 的估计,以补偿初始速度的影响。
论文中将\boldsymbol{p}_{sf}^{i_{b0}}按照三轴展开
{p}_{sf,j}^{i_{b0}} = \boldsymbol{H}\boldsymbol{\beta}_{i}+V_{i}
将初始对准问题转换为曲线拟合与参数辨识问题。
仿真验证
进行1200s的摇摆运动仿真,加入载体海上漂荡干扰,得到姿态速度变化如下图,姿态摇摆幅度大于20°,速度干扰达到5m/s。
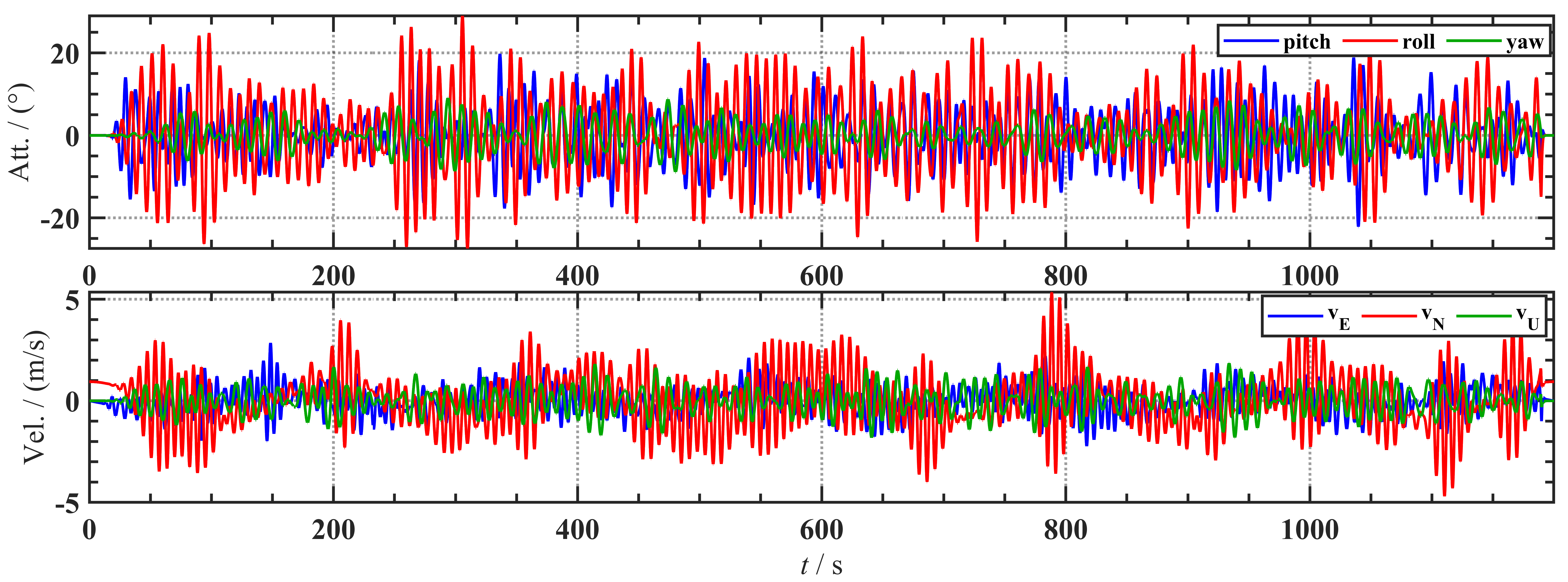
根据仿真轨迹数据,使用工具箱的反演算法得到IMU仿真数据。
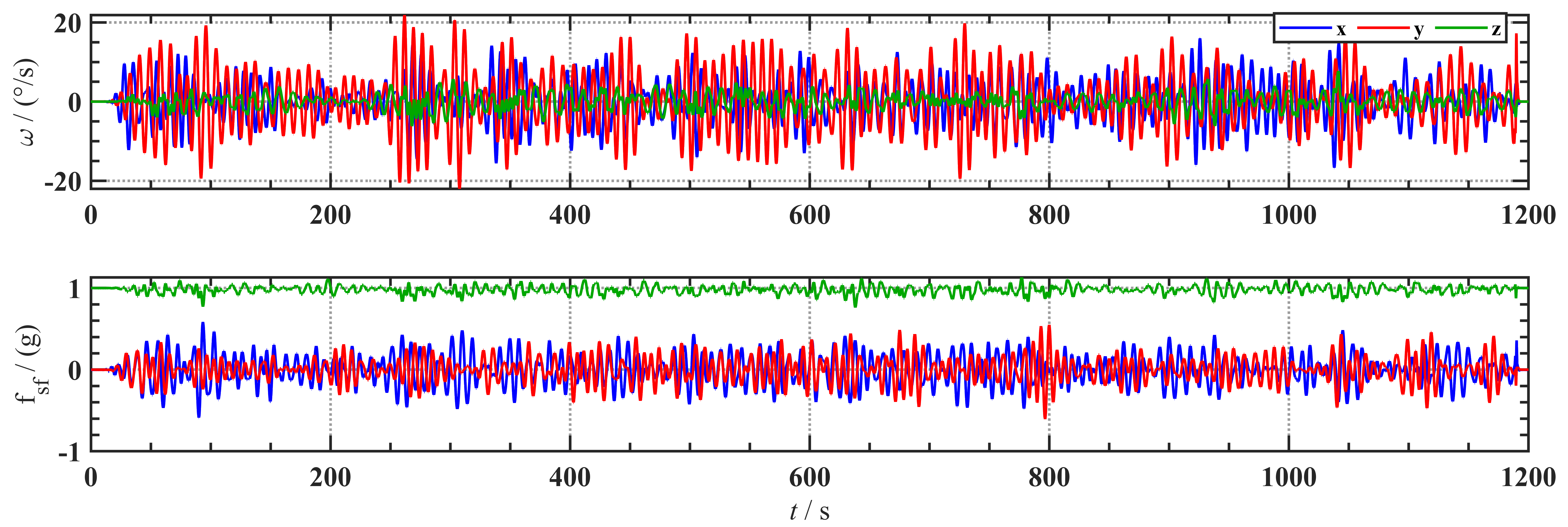
对准时注入IMU误差,其误差参数如下:
| 误差项 | 误差值 |
|---|
| 陀螺零偏 | 0.01°/h |
| 角度随机游走系数 | 0.001 \mathrm{\degree/\sqrt{h}} |
| 加速度计零偏 | 400ug |
| 速度随机游走系数 | 20 \mathrm{\mu g/\sqrt{Hz}} |
在不同纬度下进行初始对准Mont-Carlo仿真,统计初始对准误差变化如下图:
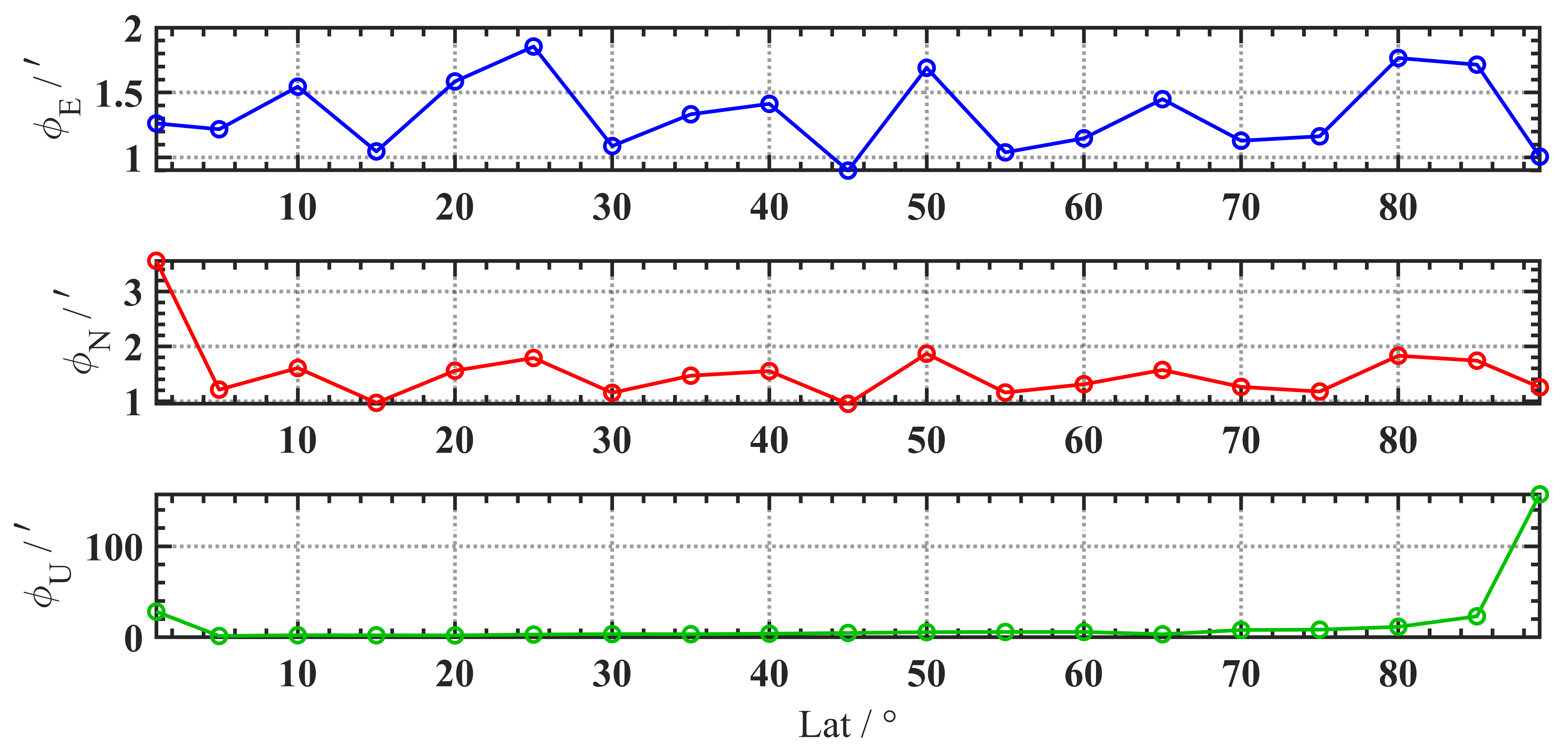
结论
纬度变化对航向对准精度影响较大,80度以上时对准精度有明显变化,85°处的航向失准角为23角分,89°处的航向失准角为157角分。
这里的仿真重点是看纬度的影响,没有对比分析不同初始速度的影响,应当补充不同初始速度下,传统算法和抗线运动算法的差异。
严老师在论文中指出“因惯性系对准方法的特点,水平失准角极限精度不只取决于加速度计零偏”,这非常适合作为一个面试题,其中包含了惯性系对准原理、对准极限精度、IMU误差特性、惯性导航误差方程等内容。
参考文献
- 严恭敏,蔺裕源,刘瑞鑫,等.抗线晃动干扰惯性系初始对准改进参数辨识方法[J].中国惯性技术学报,2023,31(05):425-430.DOI:10.13695/j.cnki.12-1222/o3.2023.05.001.
- 秦永元. (2014). 惯性导航 (第2版). 科学出版社.