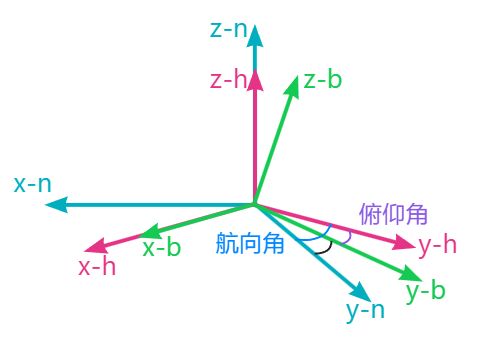
坐标系定义
IMU坐标系(b系):与IMU敏感轴重合,不考虑不正交和安装偏差,RFU;
地理坐标系(n系):东北天;
初始水平坐标系(h系):原点与b系原点重合 x轴指向 x^b 在水平面内的投影方向, z 轴指天;
角速度输出误差分析
寻北算法的关键是计算水平面内的前向轴( x^h )输出的角速度。
初始状态,IMU存在俯仰角 \theta 和偏航角 \psi ,固定此时的载体坐标系位,并定义为 b_0 系。
则 \boldsymbol{C}_{b_0}^{n}=\begin{bmatrix} \cos\psi & -\sin\psi\cos\theta & \sin\psi\sin\theta \\ \sin\psi & \cos\psi\cos\theta & -\cos\psi\sin\theta \\ 0 & \sin\theta & \cos\theta \end{bmatrix}
由 \boldsymbol{\omega}_{ie}^{b_0} = \boldsymbol{C}_{n}^{b_0} \boldsymbol{\omega}_{ie}^{n}得
\left\{\begin{aligned}\omega_{ie,x}^{b_0} &= \sin\psi \omega_y^n \\ \omega_{ie,x}^{b_0} &= \cos\psi \cos\theta \omega_y^n + \sin\theta \omega_z^n \\ \omega_{ie,z}^{b_0}&=-\cos\psi\sin\theta \omega_y^n + \cos\theta\omega_z^n \end{aligned} \right.
同理,在转过180°后,IMU处于 \pi 位置,固定此时的载体坐标系位,并定义为 b_\pi 系。
则 \boldsymbol{C}_{b_\pi}^{n}=\begin{bmatrix} -\cos\psi & \sin\psi\cos\theta & \sin\psi\sin\theta \\ -\sin\psi & -\cos\psi\cos\theta & -\cos\psi\sin\theta \\ 0 & \sin\theta & \cos\theta \end{bmatrix}
\left\{\begin{aligned}\omega_{ie,x}^{b_\pi} &= -\sin\psi \omega_y^n \\ \omega_{ie,x}^{b_\pi} &= -\cos\psi \cos\theta \omega_y^n - \sin\theta \omega_z^n \\ \omega_{ie,z}^{b_\pi}&=-\cos\psi\sin\theta \omega_y^n + \cos\theta\omega_z^n \end{aligned} \right.
将 \omega_{ie,y}^{b_0} 和 \omega_{ie,y}^{b_\pi} 简写为 \omega_{y}^{b_\pi} 和 \omega_{y}^{b_\pi} ,得
\left\{ \begin{aligned} \omega_{y}^{b_0}&= \cos\psi \cos\theta \omega_y^n + \sin\theta \omega_z^n \\ \omega_{y}^{b_\pi}&= -\cos\psi \cos\theta \omega_y^n - \sin\theta \omega_z^n \end{aligned} \right.
在IMU测量时,考虑其常值零偏 \boldsymbol{\varepsilon} 和 g 敏感性误差 \boldsymbol{\sigma} 的影响,
\left\{ \begin{aligned} \hat{\omega}_{y}^{b_0}&= \cos\psi \cos\theta \omega_y^n + \sin\theta \omega_z^n + \varepsilon_{y}^{b_0} + \sigma_{y}^{b_0}\\ \hat{\omega}_{y}^{b_\pi}&= -\cos\psi \cos\theta \omega_y^n - \sin\theta \omega_z^n + \varepsilon_{y}^{b_\pi} + \sigma_{y}^{b_\pi} \end{aligned} \right.
对于常值零偏, \varepsilon_{y}^{b_0}=\varepsilon_{y}^{b_\pi}=\bar{\varepsilon}_{y}^{b} 。
对于g敏感性误差,则有
\boldsymbol{\sigma }^{b}=\boldsymbol{K}_{G}\boldsymbol{f}^b=\boldsymbol{K}_{G}\boldsymbol{g}^b=\boldsymbol{K}_{G}\boldsymbol{C}_{n}^{b}\boldsymbol{g}^n
在0位置和 \pi 位置时,
\left\{ \begin{aligned} \boldsymbol{\sigma}^{b_0}&= \boldsymbol{K}_{G} \begin{bmatrix} 0 \\ \sin\theta \cdot g \\ \cos\theta \cdot g\end{bmatrix} = \begin{bmatrix} k_{12}\sin\theta g + k_{13}\cos\theta g \\ k_{22}\sin\theta g + k_{23}\cos\theta g \\ k_{32}\sin\theta g + k_{33}\cos\theta g\end{bmatrix}\\ \boldsymbol{\sigma}^{b_\pi}&= \boldsymbol{K}_{G} \begin{bmatrix} 0 \\ -\sin\theta \cdot g \\ \cos\theta \cdot g\end{bmatrix} = \begin{bmatrix} -k_{12}\sin\theta g + k_{13}\cos\theta g \\ -k_{22}\sin\theta g + k_{23}\cos\theta g \\ -k_{32}\sin\theta g + k_{33}\cos\theta g\end{bmatrix}\end{aligned}\right.
将误差代入角速度量测可得
\left\{ \begin{aligned} \hat{\omega}_{y}^{b_0}&= \cos\psi \cos\theta \omega_y^n + \sin\theta \omega_z^n + \bar{\varepsilon}_{y}^{b} + k_{22}\sin\theta g + k_{23}\cos\theta g\\ \hat{\omega}_{y}^{b_\pi}&= -\cos\psi \cos\theta \omega_y^n - \sin\theta \omega_z^n + \bar{\varepsilon}_{y}^{b} -k_{22}\sin\theta g + k_{23}\cos\theta g \end{aligned} \right.
两式相减,得
\hat{\omega}_{y}^{b_0}-\hat{\omega}_{y}^{b_\pi} = 2\cos\psi \cos\theta \omega_y^n + 2\sin\theta \omega_z^n + 2 k_{22}\sin\theta g
\hat{\omega}_{y}^{b_0}-\hat{\omega}_{y}^{b_\pi} - 2\sin\theta \omega_z^n - 2 k_{22}\sin\theta g= 2\cos\psi \cos\theta \omega_y^n
\cos\psi = \frac{\hat{\omega}_{y}^{b_0}-\hat{\omega}_{y}^{b_\pi} - 2\sin\theta \omega_z^n - 2 k_{22}\sin\theta g}{2\cos\theta \omega_y^n}
同理可得, \sin\psi=\frac{\omega_{x}^{b_0}-\omega_{x}^{b_\pi}-2k_{12}\sin\theta g}{2\omega_{y}^{n}}
因此,
\tan\psi=\frac{\left(\omega_{x}^{b_0}-\omega_{x}^{b_\pi}-2k_{12}\sin\theta g\right) \cos\theta } {\hat{\omega}_{y}^{b_0}-\hat{\omega}_{y}^{b_\pi} - 2\sin\theta \omega_z^n - 2 k_{22}\sin\theta g}
航向测量值为
\hat{\boldsymbol{\psi}}=\arctan\left[\frac{\left(\omega_{x}^{b_0}-\omega_{x}^{b_\pi}-2k_{12}\sin\theta g\right) \cos\theta } {\hat{\omega}_{y}^{b_0}-\hat{\omega}_{y}^{b_\pi} - 2\sin\theta \omega_z^n - 2 k_{22}\sin\theta g}\right]
若没有g敏感性误差,则
{\boldsymbol{\psi}}=\arctan\left[\frac{\left(\omega_{x}^{b_0}-\omega_{x}^{b_\pi}\right) \cos\theta } {\hat{\omega}_{y}^{b_0}-\hat{\omega}_{y}^{b_\pi} - 2\sin\theta \omega_z^n }\right]
令 w_y=\omega_{x}^{b_0}-\omega_{x}^{b_\pi} , w_y=\omega_{y}^{b_0}-\omega_{y}^{b_\pi} , v_z=2\sin\theta\omega_{z}^{n} , g_x=2k_{12}\sin\theta g , g_y=2k_{22}\sin\theta g ,得
\delta\psi=\frac{\cos\theta\left(g_xv_z-g_xw_y+w_xg_y\right)}{\left(w_y-v_z-g_y\right)\left(w_y-v_z\right)}
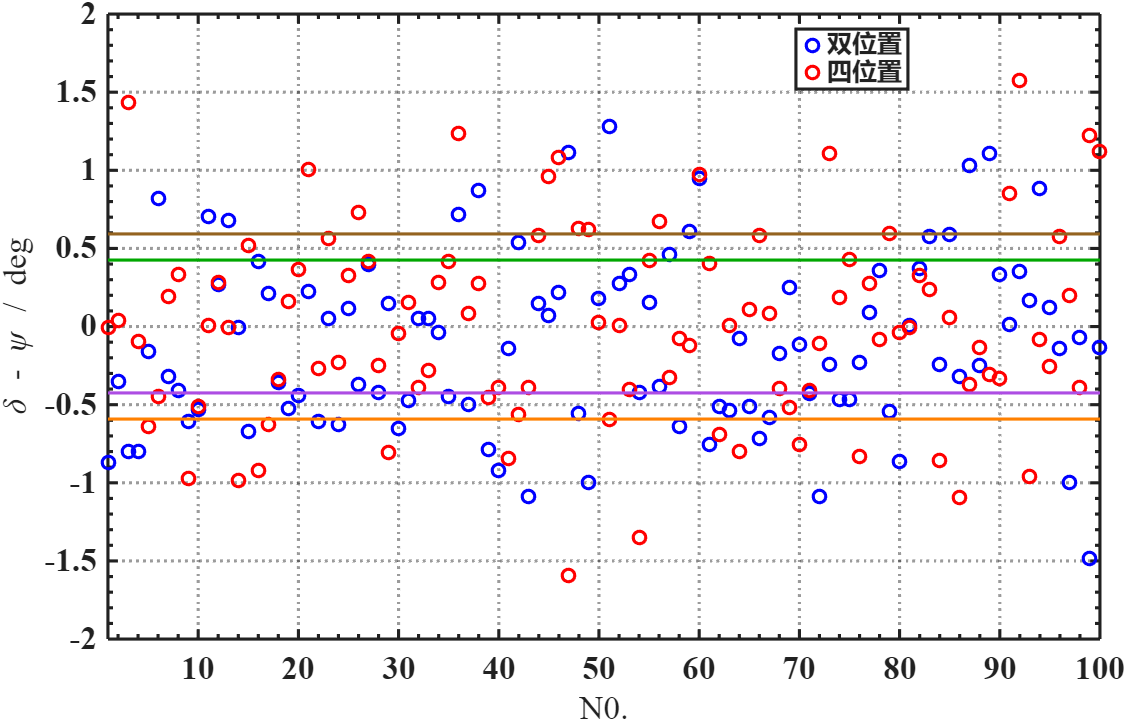
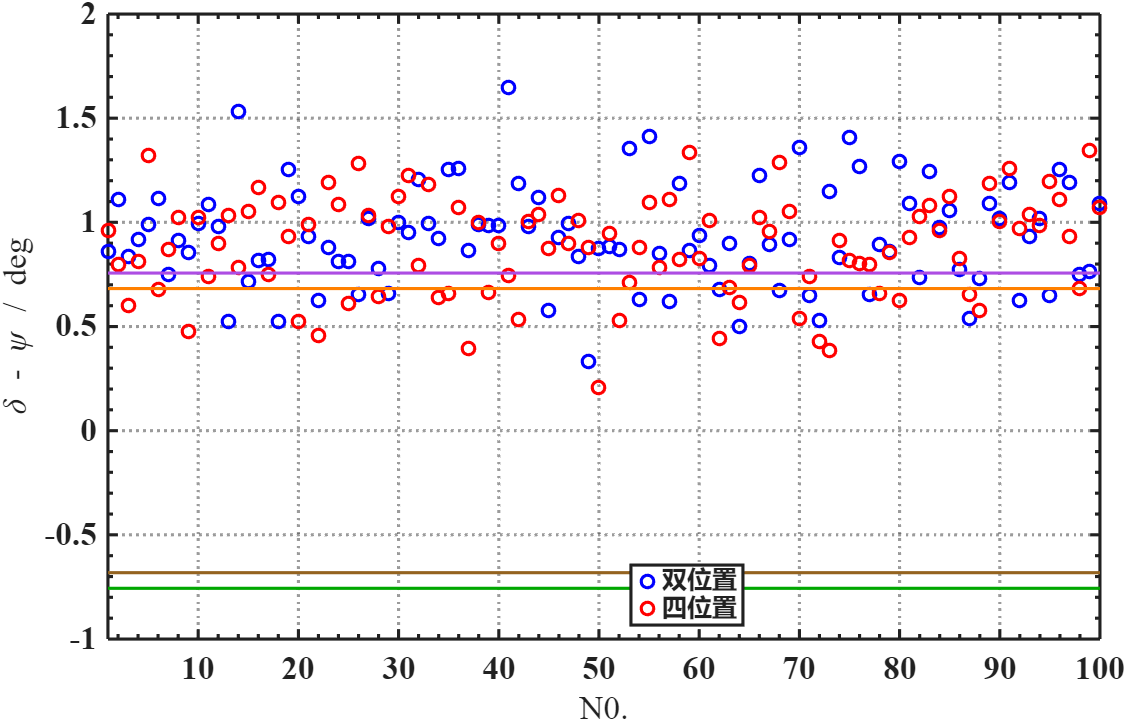
仿真验证
在俯仰角30°条件下,进行寻北仿真。
仿真程序:
% ------------------------------------------------------------------------
% Filename: notth_finder_gsen.m
%
% Description:
% 分析陀螺g敏感性误差对于寻北的影响
%
% Author: TMRNic
% Contact: yangxk@mail.nwpu.edu.cn
% Date: 2024-11-09
% ------------------------------------------------------------------------
start; % 初始化
ts = 0.010; % 采样周期
pitch = 30*glv.deg; % 俯仰角
att = [pitch 0 0; -pitch 0 pi; 0 -pitch pi/2; 0 pitch 3*pi/2]; % 寻北位置的姿态角
eth = earth(glv.pos0); % 地球模型
wnie = eth.wnie.*ts; % 地球自转
gn = -eth.gn.*ts; % 重力
imu = zeros(4000,7); % 初始化IMU数据
idx_int = zeros(4,2); % 每个IMU数据区间
for k=1:4
Cnb = a2mat(att(k,:)); % 姿态角转矩阵
wbie = Cnb'*wnie; % b系地球自转
fbsf = Cnb'*gn; % b系比力
imu(1000*(k-1)+1:1000*k, 1:6) = repmat([wbie; fbsf]', 1000,1); % IMU数据
idx_int(k,:) = [1000*(k-1)+1, 1000*k]; % IMU数据区间
end
imu(:,7) = (1:4000).*ts; % 时间
KG = [10 1 1; 1 30 1; 1 1 10].*glv.dph.*ts; % 陀螺重力敏感误差
imuerr = imuerrset(0.1, 1000, 0.01, 10); % 初始化IMU误差
imu(:,1:3) = imu(:,1:3) + imu(:,4:6)*KG'./ts./glv.g0; % 加入重力敏感误差
nMC = 200; % 模拟次数
psi_res = zeros(nMC,2); % 初始化结果
for kMC = 1:nMC
imuk = imuadderr(imu, imuerr); % 加入IMU误差
omgb = zeros(4,3); % 初始化四组陀螺角速度
for k=1:4
omgb(k,:) = mean(imuk(idx_int(k,1):idx_int(k,2),1:3)./ts./glv.dph); % 计算四组陀螺角速度
omgb(k,:) = omgb(k,:)*a2mat([att(k,1:2),0]); % 转至水平系
end
% 双位置
wb = 0.5*(omgb(1,:)-omgb(2,:))';
psi2 = atan(wb(1)/wb(2))./glv.deg;
% 四位置
eth = earth(glv.pos0);
wb13 = 0.5*(omgb(1,:)-omgb(2,:));
wb24 = 0.5*(omgb(3,:)-omgb(4,:));
wsL = glv.wie./glv.dph.*eth.cl;
psi4 = atan(wb24(2)/wb13(2))./glv.deg;
% 计算结果
psi_res(kMC, :) = [psi2, psi4];
end
% 绘图
figure;
plotEx((1:100), psi_res, 'o'); hold on;
plotEx([1;100], [-psi2 psi2 psi4 -psi4; -psi2 psi2 psi4 -psi4]);
xylabelsEx('N0.','\delta - \psi / deg');
legendEx({'双位置','四位置'});
% 计算RMS
psi_rms = rms(psi_res);
disp(psi_rms);
| 双位置 | 四位置 |
|---|
| 不加入g敏感性误差 | 0.5795° | 0.6060° |
| 加入g敏感性误差 | 0.9513° | 0.9399° |