Kalman滤波、自适应KF滤波与H∞滤波
Kalman滤波在线性动态系统中对未知状态变量进行最优估计,通过最小化估计误差的协方差来实现状态的最优估计。分为预测和更新两个主要步骤。预测步骤根据上一个时刻的最优估计预测当前时刻的状态变量,而更新步骤则根据当前时刻的观测数据对预测状态进行修正。
自适应卡尔曼滤波器能够在利用测量数据进行滤波的同时,不断地由滤波本身去判断系统的动态是否有变化,对模型参数和噪声统计特性进行估计和修正,以改进滤波设计、缩小滤波的实际误差
H∞滤波是一种鲁棒滤波方法,适用于存在不确定性和噪声的系统。它通过优化系统的鲁棒性能来实现状态估计,特别适合于复杂和不确定的环境。H∞滤波在设计时考虑了最坏情况下的噪声影响,因此具有较强的鲁棒性。它能够在噪声统计特性不确定或变化的情况下保持较好的滤波性能。
总的来说,Kalman滤波适用于线性系统且噪声统计特性已知的情况;自适应滤波则更灵活,能够适应输入信号的变化;而H∞滤波则强调鲁棒性,适用于噪声统计特性不确定或变化较大的情况。在实际应用中,应根据具体需求选择合适的滤波方法。
【疑问】从定义上或者形式上来判断,H∞滤波是否属于Kalman滤波的一种呢?
简答三维线性系统举例
模型说明
一个三维系统的系统方程和量测方程如下:
\begin{bmatrix} \dot{x}_1 \\ \dot{x}_2 \\ \dot{x}_3\end{bmatrix} = \begin{bmatrix} 0 & 0.01 & 0 \\ 0 & 0 & 0.1 \\ 0 & 0 & 0 \end{bmatrix}\begin{bmatrix} {x}_1 \\ {x}_2 \\ {x}_3\end{bmatrix} + \begin{bmatrix} 0\\ w_1 \\ w_2 \end{bmatrix}
\begin{bmatrix} {z}_1 \\{z}_2\end{bmatrix} = \begin{bmatrix} 0.7 & 0.3 & 0\\ 0&0&1\end{bmatrix}\begin{bmatrix} {x}_1 \\ {x}_2 \\ {x}_3\end{bmatrix} + \begin{bmatrix} {v}_1 \\ {v}_2 \end{bmatrix}
系统采样间隔ts=0.01s,系统噪声w1和w2的方差为0.01和0.01;量测噪声v1和v2的方差为0.1和0.1,在10-12s之间,噪声v2的方差扩大了10倍。
状态变化图如下:
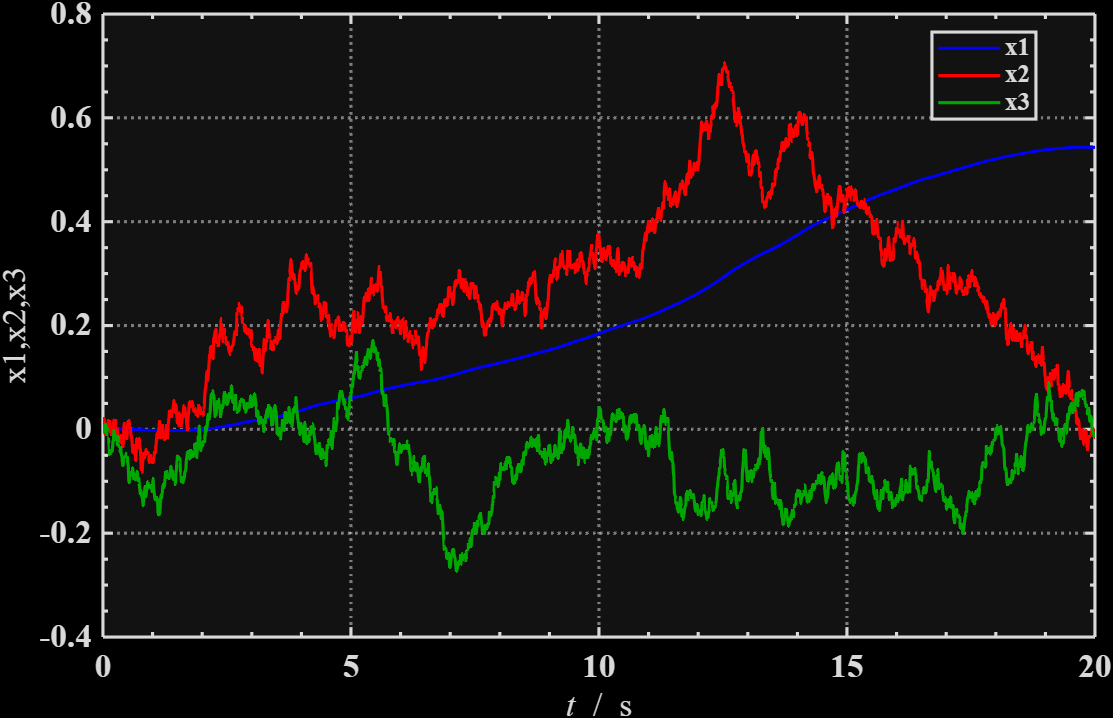
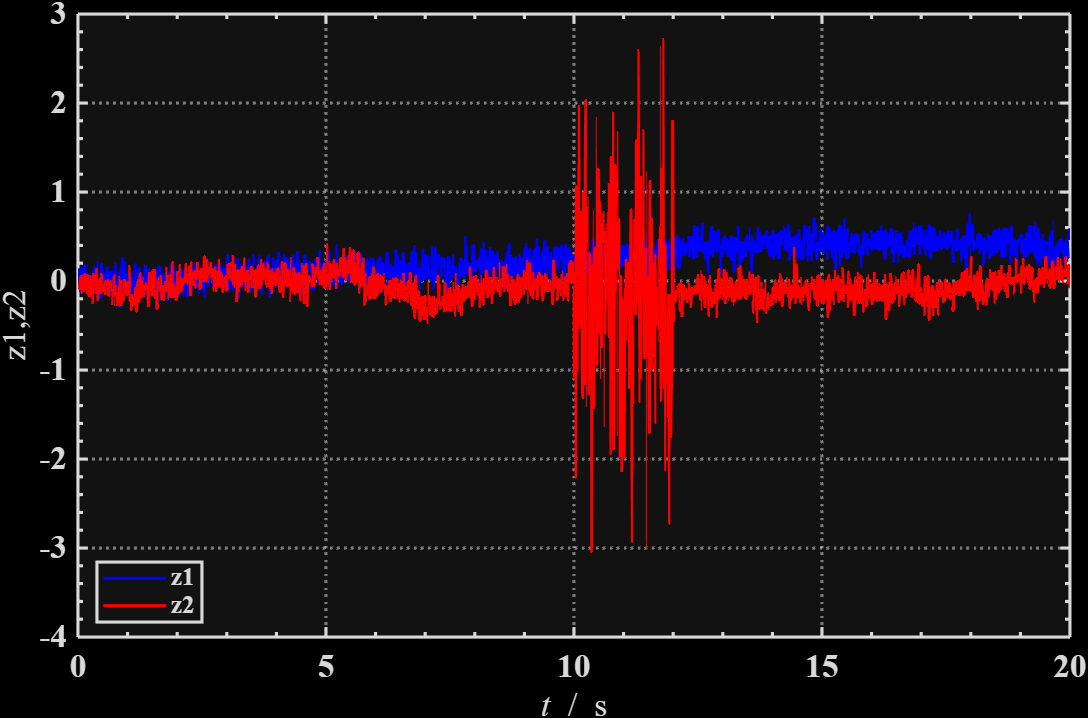
量测变化图如下,显然在10-12s之间z2的噪声变大。
滤波仿真
使用标准卡尔曼滤波(StdKF)、H∞滤波(H-inf)和自适应滤波(AFFKF)进行状态估计,得到状态估计和状态估计误差变化如下。
| 状态估计误差 | 标准Kalman滤波 | 自适应滤波 | H∞滤波 |
|---|
| RMS-\delta x_1 | 0.0364 | 0.0406 | 0.0363 |
| RMS-\delta x_2 | 0.1013 | 0.1143 | 0.1012 |
| RMS-\delta x_3 | 0.0871 | 0.0519 | 0.0596 |
仿真程序如下,代码中可能有一些我自己的函数,导致无法运行,程序非常简单,稍加修改即可正常运行。
%% ======================================================= %
% Kalman Filtering & H-infinity Filter %
% Author: TMRNic %
% Date: 2024-10-29 %
% Description: %
% 1. 10s-12s 量测z2的噪声变大 %
% 2. 状态空间模型 %
% |dx1/dt| |0 0.1 0 ||x1| |0 | %
% |dx2/dt| = |0 0 0.1||x2|+|w1| %
% |dx3/dt| |0 0 0 ||x3| |w2| %
% |x1| %
% |z1| = |0.7 0.3 0||x2|+|v1| %
% |z2| | 0 0 1||x3| |v2| %
% ================================================================ %
addpath SubFunctions\;
clc; clear; close all; % Clear all variables from workspace
glvs;
T = 20; % 时间长度
ts = 0.01; % 采样间隔
len = floor(T/ts); % 采样点数
M = 3; N = 2; % 状态维数,观测维数
load test_data.mat; % 加载数据
%% STD-KF =========================================================== %
xk = zeros(M,1); % 初始状态
pk = diag([1,1,1]); % 初始状态误差协方差
Qk = diag(QV.^2); % 系统噪声方差
Rk = diag(RV.^2); % 观测噪声方差
Hk = [0.7 0.3 0; 0 0 1]; % 观测矩阵
xkpk = zeros(len, M+M+1); % 状态和方差存储矩阵
for k=1:len
xkk_1 = Phi*xk; % 状态预测
pkk_1 = Phi*pk*Phi' + Qk; % 方差预测
zk = xkzk(k,4:5)'; % 观测向量
kk = pkk_1*Hk'*invbc(Hk*pkk_1*Hk'+Rk); % 滤波增益
xk = xkk_1 + kk*(zk-Hk*xkk_1); % 状态更新
pk = (eye(M)-kk*Hk)*pkk_1; % 方差更新
xkpk(k,:) = [xk; diag(pk); k*ts]; % 状态和方差存储
end
%% H-inf-KF ========================================================== %
xk = zeros(M,1);
pk = diag([1,1,1]);
Qk = diag(QV.^2);
Rk = diag(RV.^2);
gamma2 = 0.0;
Lk = [0 0 1];
Re0 = zeros(3); Re0(1:2,1:2) = Rk; Re0(3,3) = -gamma2;
xkpk_hinf = zeros(len, M+M+1);
for k=1:len
xkk_1 = Phi*xk;
pkk_1 = Phi*pk*Phi' + Qk;
zk = xkzk(k,4:5)';
% ================== H infity filter process ==================== %
Rek = Re0 + [Hk; Lk]*pkk_1*[Hk; Lk]';
kk = pkk_1*Hk'*invbc(Rk+Hk*pkk_1*Hk'); % 滤波增益
pk = pkk_1 - pkk_1*[Hk; Lk]'*invbc(Rek)*[Hk; Lk]*pkk_1;
xk = xkk_1 + kk*(zk-Hk*xkk_1);
% =============================================================== %
xkpk_hinf(k,:) = [xk; diag(pk); k*ts];
end
%% AFFKF =========================================================== %
xk = zeros(M,1);
pk = diag([1,1,1]);
Qk = diag(QV.^2);
Rk = diag(RV.^2);
xkpk_af = zeros(len, M+M+1);
for k=1:len
xkk_1 = Phi*xk;
pkk_1 = Phi*pk*Phi' + Qk;
zk = xkzk(k,4:5)';
pzz = Hk*pkk_1*Hk'+Rk;
inv_zk = zk-Hk*xkk_1;
sigma = inv_zk'*invbc(pzz)*inv_zk;
alpha = 1-exp(-0.1/sigma);
bk = 0.97+alpha*0.299;
dk = (1-bk)/(1-bk^k);
Rk = (1-dk)*Rk + dk*(inv_zk*inv_zk'-Hk*pkk_1*Hk');
kk = pkk_1*Hk'*invbc(pzz);
xk = xkk_1 + kk*(inv_zk);
pk = (eye(M)-kk*Hk)*pkk_1;
xkpk_af(k,:) = [xk; diag(pk); k*ts];
end
%% Plot result ====================================================== %
err = [xkpk(:,1:3)-xkzk(:,1:3) xkpk_hinf(:,1:3)-xkzk(:,1:3) xkpk_af(:,1:3)-xkzk(:,1:3)];
rmse = reshape(rms(err), 3, []);
myfigure;
subplot(231);
plotEx(xkzk(:,end), [xkzk(:,1),xkpk(:,1), xkpk_hinf(:,1),xkpk_af(:,1)],'--'); % Plot state -x1
xylabelsEx('x1'); legendEx({'Ref.','StdKF','H-inf','AFFKF'});
subplot(232);
plotEx(xkzk(:,end), [xkzk(:,2),xkpk(:,2), xkpk_hinf(:,2),xkpk_af(:,2)],'--'); % Plot state -x2
xylabelsEx('x2'); legendEx({'Ref.','StdKF','H-inf','AFFKF'});
subplot(233);
plotEx(xkzk(:,end), [xkzk(:,3),xkpk(:,3), xkpk_hinf(:,3),xkpk_af(:,3)],'--'); % Plot state -x3
xylabelsEx('x3'); legendEx({'Ref.','StdKF','H-inf','AFFKF'});
subplot(234);
plotEx(xkzk(:,end), err(:,1:3:end)); % Plot estimation error -x1
xylabelsEx('\delta x1'); legendEx({'StdKF','H-inf','AFFKF'});
subplot(235);
plotEx(xkzk(:,end), err(:,2:3:end)); % Plot estimation error -x2
xylabelsEx('\delta x2'); legendEx({'StdKF','H-inf','AFFKF'});
subplot(236);
plotEx(xkzk(:,end), err(:,3:3:end)); % Plot estimation error -x3
xylabelsEx('\delta x3'); legendEx({'StdKF','H-inf','AFFKF'});
传递对准举例
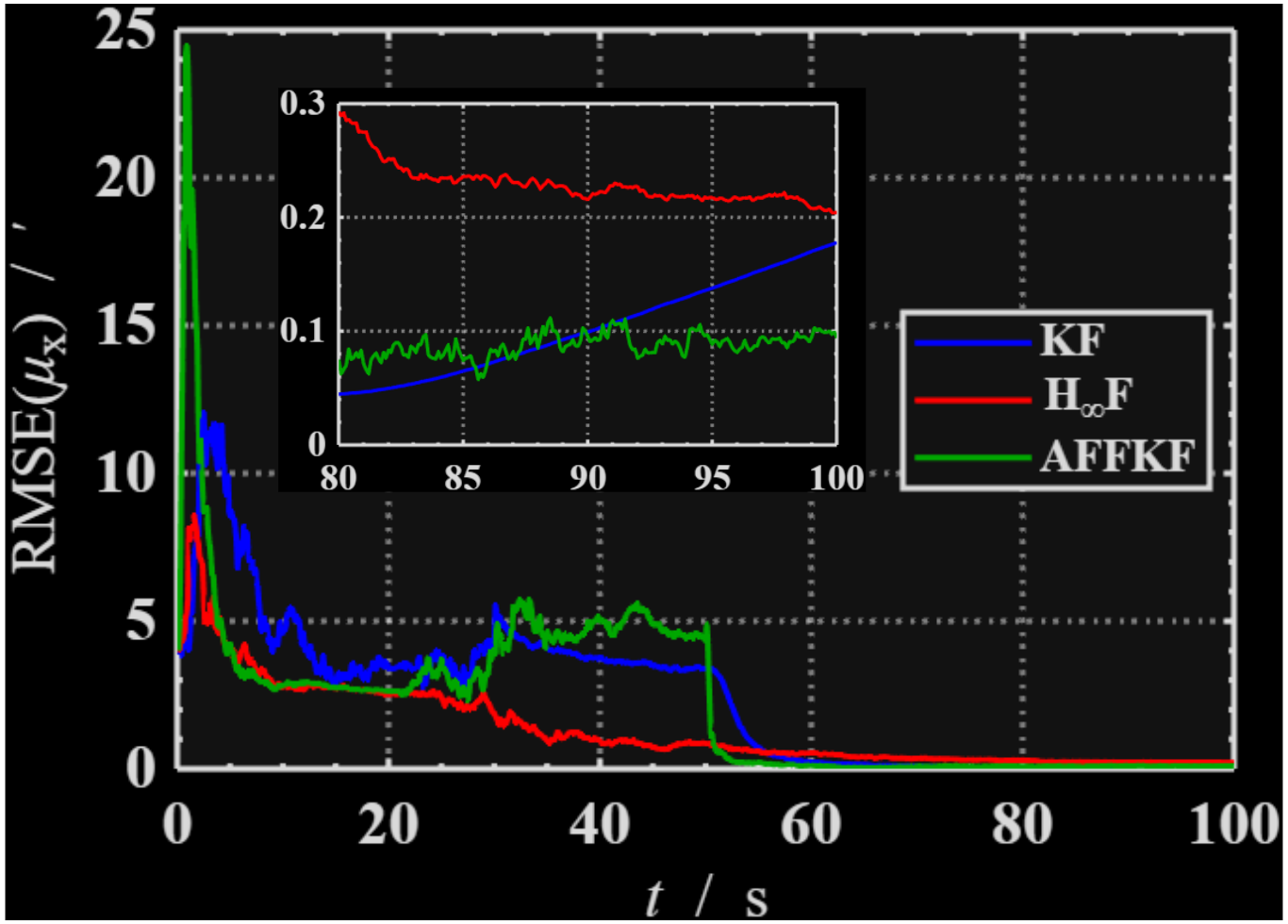
传递对准中往往存在挠曲变形等干扰,严重影响滤波器的状态估计精度。下文给出有一组传递对准仿真数据处理结果,分别用标准KF,自适应KF和H∞滤波进行安装偏角的估计,得到主子惯导安装偏角估计误差变化如下图所示。
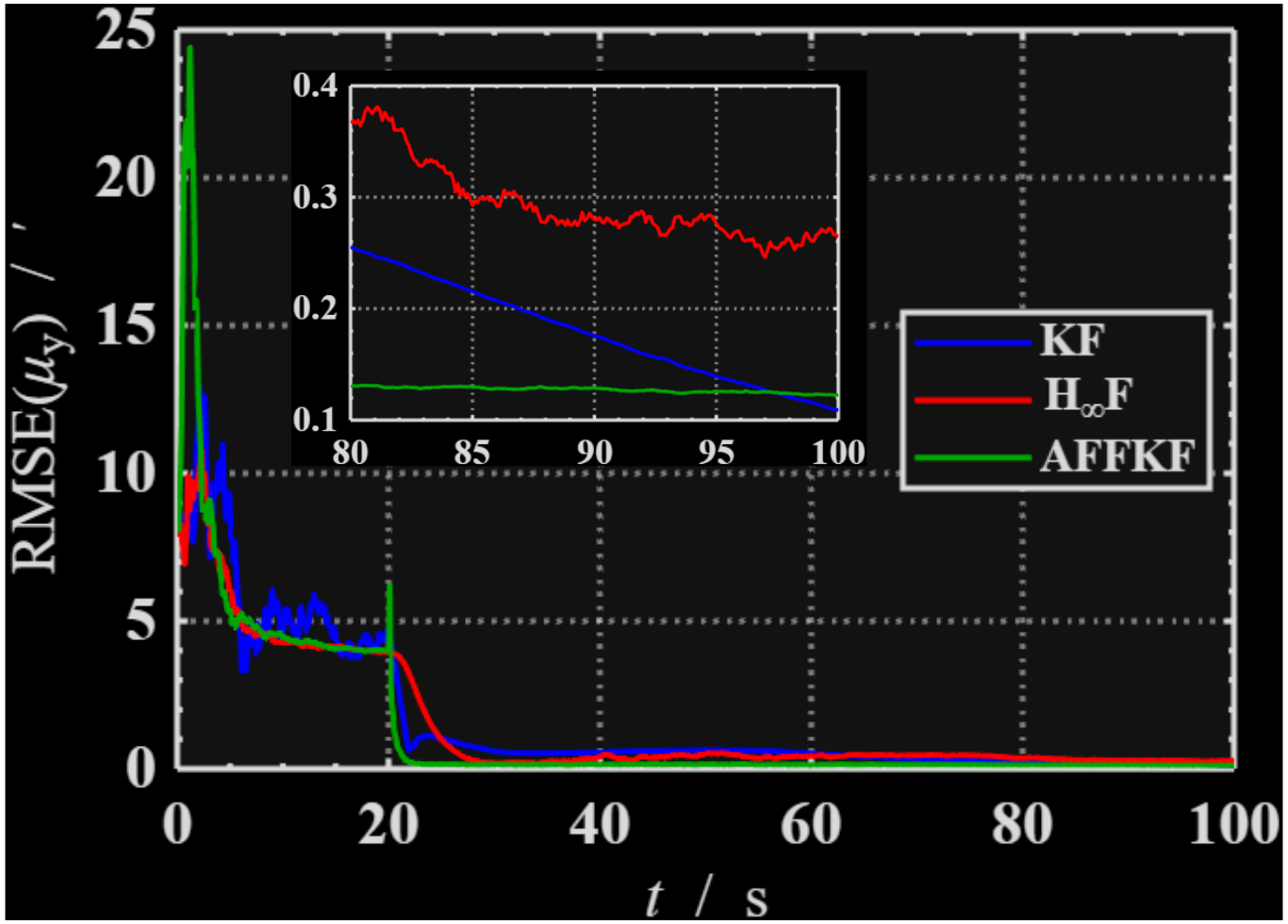
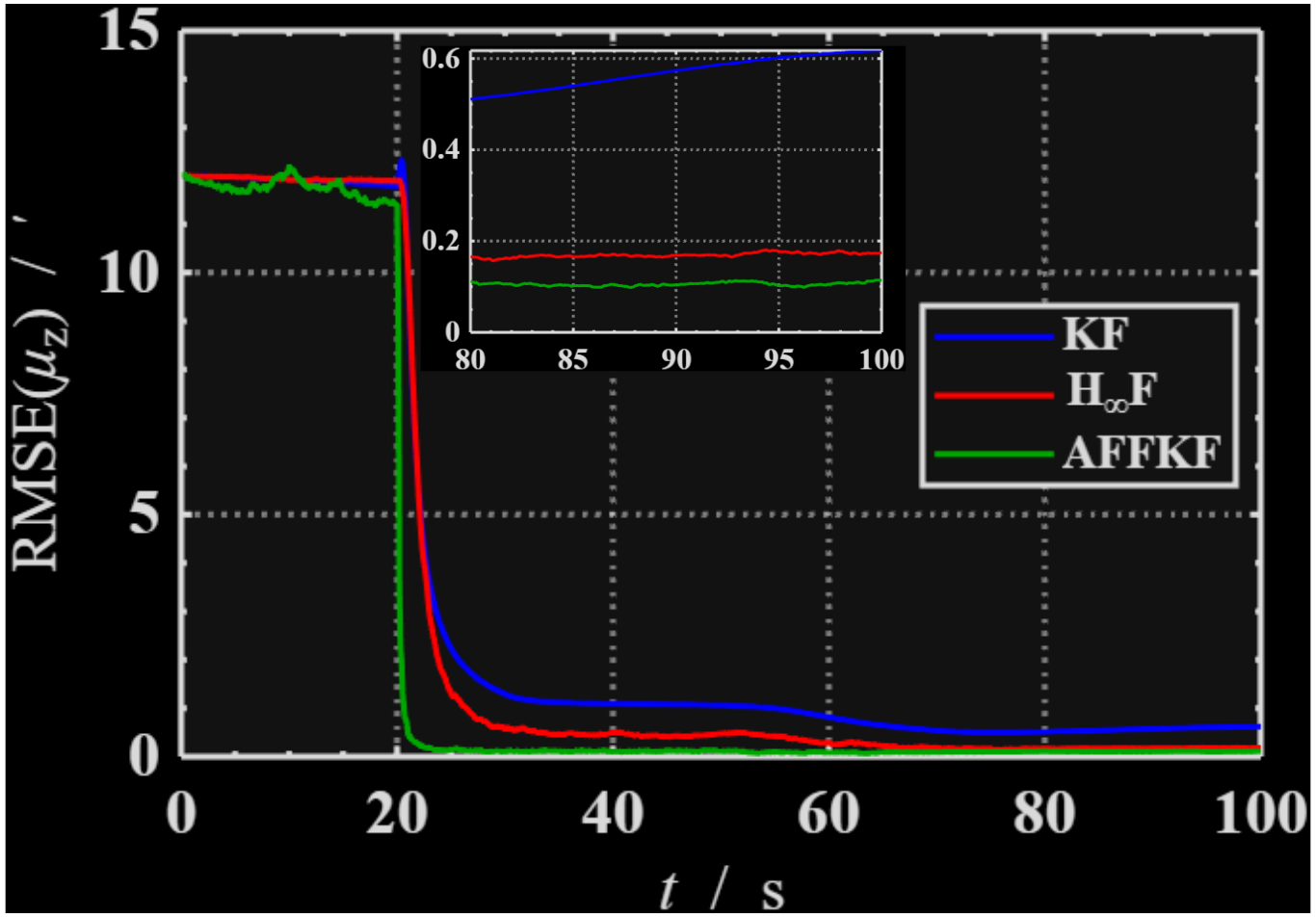
结论
根据两组仿真结果,三种状态估计方法的表现与预期一致。具体而言:
● 标准卡尔曼滤波在噪声强度恒定的线性系统中表现出色,能够提供较为准确的状态估计。然而,该方法缺乏对模型动态变化的适应能力。其优势在于算法结构简单且需要调整的参数较少。
● 自适应卡尔曼滤波通过在滤波更新过程中依据预测值与实际测量值之间的偏差来调整测量噪声方差,从而实现了对噪声强度变化的有效跟踪。
● H∞滤波则无需引入额外的测量误差参数估计步骤,在设计阶段选择重点关注的状态变量或状态组合以提高这些特定状态估计的稳定性。这使得H∞滤波具有良好的鲁棒性,但其参数调节过程相对复杂。
对于大多数应用场景而言,采用标准卡尔曼滤波已足够满足需求;当面临系统异常情况时,可借助故障检测与隔离(FDFI)技术减轻异常因素对滤波性能的影响,此方法相较于自适应滤波内部自我调整机制可能更为可靠。尽管从理论上讲,H∞滤波具备强大的抗干扰能力,但在实际应用中仍需细致地针对具体模型进行参数设定,并且该方法对参数设置更加敏感。因此,在工程实践中,考虑到实施便捷性和有效性,推荐优先选用标准卡尔曼滤波;若模型及其相关参数存在轻微变动,则可以考虑使用自适应卡尔曼滤波;而目前来看,H∞滤波尚不具备广泛应用于现实系统的条件。
参考文献
● Li, W., & Jia, Y. (2010). H-infinity filtering for a class of nonlinear discrete-time systems based on unscented transform. Signal Processing
● 严恭敏,翁浚. (2019). 捷联惯导算法与组合导航原理 (第1版). 西北工业大学出版社.
● 张勇刚, 李宁, & 奔粤阳. (2013). 最优状态估计: 卡尔曼, H∞ 及非线性滤波. 北京: 国防工业出版社